下面程序是判断一个点能否在矩阵内部的,但是由于小弟的数学是在是糟糕,所以请数学高手来指点迷津
题目如下:
一个矩阵可以用4个点代表,(x1,y1)代表最上面的点,(x2,y2)代表最上面的点,(x3,y3)代表最下面的点,(x4,y4)代表最右的点。给定这4个点代表一个矩形,在给定一个点,判断(x,y)能否在矩形中。
下面这是矩形的边平行于坐标轴时的代码
题目如下:
一个矩阵可以用4个点代表,(x1,y1)代表最上面的点,(x2,y2)代表最上面的点,(x3,y3)代表最下面的点,(x4,y4)代表最右的点。给定这4个点代表一个矩形,在给定一个点,判断(x,y)能否在矩形中。
下面这是矩形的边平行于坐标轴时的代码
ool _IsInside(double x1, double y1, double x4, double y4,double x,double y)
{
if (x <= x1)
{
return false;
}
if (x >= x4)
{
return false;
}
if (y >= y1)
{
return false;
}
if (y <= y4)
{
return false;
}
return true;
}
,
下面这时不平行与坐标轴时的代码。
解释是:根据高中数学的知识,通过坐标变换把矩阵转成平行的情况,在旋转时全部点也跟着转动就可以了
bool IsInside(double x1, double y1, double x2, double y2, double x3, double y3, double x4, double y4, double x, double y)
{
if (y1 == y2)
{
return _IsInside(x1, y1, x4, y4, x, y);
}
double l = abs(y4 - y3);
double k = abs(x4 - x3);
double s = sqrt(k*k + l*l);
double sin = l / s;
double cos = k / s;
double x1R = cos*x1 + sin*y1;
double y1R = -x1*sin + y1*cos;
double x4R = cos*x4 + sin*y4;
double y4R = -x4*sin + y4*cos;
double xR = cos*x + sin*y;
double yR = -x*sin + y*cos;
return _IsInside(x1R, y1R, x4R, y4R, xR, yR);
}
请解释一下上述的变换到底是怎么回事,最好可以画个图,小弟的数学实在是太差了
解决方案
40
假如是任意4个点组成的四边形,可将问题转换成计算三角形面积
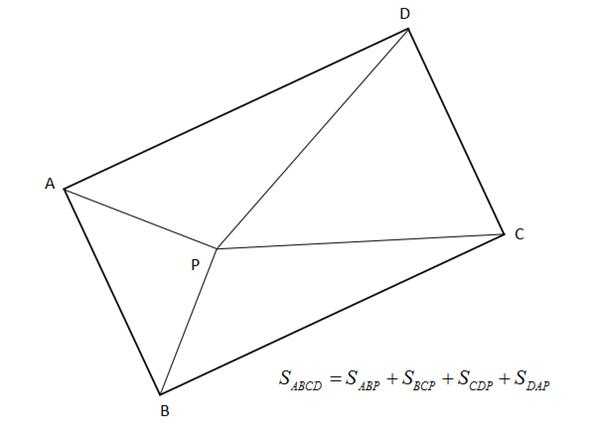
1、AB与CD相交,非四边形
2、ABC组成的三角形面积,与ABD、ACD、BCD三个三角形面积之和比较,假如相等,为凸四边形,面积为ABC和ADC之和,假如大于,为两者之差
3、比较ABP、BCP、CDP、DAP四个三角形面积之和与四边形面积,若大于P在四边形ABCD之外,否则之内

1、AB与CD相交,非四边形
2、ABC组成的三角形面积,与ABD、ACD、BCD三个三角形面积之和比较,假如相等,为凸四边形,面积为ABC和ADC之和,假如大于,为两者之差
3、比较ABP、BCP、CDP、DAP四个三角形面积之和与四边形面积,若大于P在四边形ABCD之外,否则之内