> C语言 > 链表一元多项式乘法, 乘法运行错误，想不通哪里的问题，求帮助

链表一元多项式乘法, 乘法运行错误，想不通哪里的问题，求帮助

C语言 码拜 9年前 (2016-04-16) 990次浏览 
/*
*02-线性结构1 一元多项式的乘法与加法运算
*本人采用的是不带头结点的单向链表表示多项式
*/
# include <stdio.h>
# include <stdlib.h>
typedef struct Node * List;
struct Node{
	int xishu;
	int zhishu;
	List next;
};
typedef struct Node Node;
//求表长
int getLength(List list){
	if(list == NULL)
		return 0;
	int length = 0;
	List p = list;
	while(p){	//到达尾结点
		length ++;
		p = p->next;
	}
	return length;
}
//遍历一个链表
void print(List list){
	if(NULL == list)
		printf("0 0");
	List p = list;
	int flag = 0;
	while(p){
		if(flag)
			printf(" ");
		else
			flag = 1;
		printf("%d %d",p->xishu,p->zhishu);
		p = p->next;
	}
}
//在最后添加一个结点
List insert(List list, List target){
	if(list == NULL){
		list = target;
		return list;
	}else{
		List p = list;
		while(p->next != NULL){
			p = p->next;	//p指向当前链表的最后一个结点
		}
		p->next = target;
		return list;	//返回插入后的新链表
	}
}
//两个链表相加
List add(List a_list, List b_list){
	List sum = NULL, i = a_list, j = b_list, val;
	while(i && j){
		if(i->zhishu > j->zhishu){
			val = (List)malloc(sizeof(Node));
			val->xishu = i->xishu;
			val->zhishu = i->zhishu;
			val->next = NULL;
			sum = insert(sum,val);
			i = i->next;
		}else if(i->zhishu < j->zhishu){
			val = (List)malloc(sizeof(Node));
			val->xishu = j->xishu;
			val->zhishu = j->zhishu;
			val->next = NULL;
			sum = insert(sum,val);
			j = j->next;
		}else{		//指数相等的时候
			List newNode = (List)malloc(sizeof(Node));
			newNode->xishu = i->xishu + j->xishu;
			newNode->zhishu = i->zhishu;
			newNode->next = NULL;
			sum = insert(sum, newNode);
			i = i->next;
			j = j->next;
		}
	}
	while(i){
		sum = insert(sum, i);
		i = i->next;
	}
	while(j){
		sum = insert(sum, j);
		j = j->next;
	}
	return sum;
}
//两个链表相乘
List mul(List a_list, List b_list){
	List product = NULL;	//存放最终结果 
	List temp = NULL;	//存放内层循环结果
	List i = a_list, j = b_list;

	List newNode;
	while(i){
		j=b_list;		//这一步千万不要忘记了
		temp = NULL;
		while(j){
			newNode = (List)malloc(sizeof(Node));
			newNode->xishu = i->xishu * j->xishu;
			newNode->zhishu = i->zhishu + j->zhishu;
			newNode->next = NULL;

			j = j->next;
			product = insert(product,newNode);
			//temp = insert(temp,newNode);
		}
		//product = add(product, temp);		//每个内层循环完之后，与最终结果归并一次
		i = i->next;
	}
	return product;
}
//test
int main (void){
	int a_length, b_length;
	List a_list = NULL,b_list = NULL;
	List sum, product;	//存放结果
	//输入a链表
	scanf("%d", &a_length);
	for(int i=0; i<a_length; i++){
		List newNode = (List)malloc(sizeof(Node));
		scanf("%d%d", &newNode->xishu, &newNode->zhishu);
		newNode->next = NULL;
		a_list = insert(a_list, newNode);
	}
	//输入b链表
	scanf("%d", &b_length);
	for(int j=0; j<b_length; j++){
		List newNode = (List)malloc(sizeof(Node));
		scanf("%d%d", &newNode->xishu, &newNode->zhishu);
		newNode->next = NULL;
		b_list = insert(b_list, newNode);
	}
	//print(a_list);
	//print(b_list);
	sum = add(a_list,b_list);
	product = mul(a_list,b_list);

	print(product);
	printf("\n");
	print(sum);
	return 0;
}
解决方案

5

仅供参考：

//链表实现一元多项式的加法减法乘法
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
    float coef;   //系数
    int expn;     //指数
    struct node *next;
}
PolyNode;      //多项式节点 polynomial node
typedef PolyNode* Polynomial;
Polynomial createPolynomial() {  //创建多项式
    PolyNode *p, *q, *head = (PolyNode *)malloc(sizeof(PolyNode));   //头节点
    head->next = NULL;
    float coef;
    int expn;
    printf("输入该多项式每一项的系数和指数，每项一行，输入0 0结束！\n");
    while (scanf("%f %d", &coef, &expn) && coef) {   // 默认，按指数递减排列
        if (head->next) {
            p = head;
            while (p->next && expn < p->next->expn)
                p = p->next;
            if (p->next) {
                if (expn == p->next->expn) { //有相同指数的直接把系数加到原多项式
                    p->next->coef += coef;
                    if (p->next->coef > -0.000001 && p->next->coef < 0.000001) { //若是相加后系数为0，则舍弃该节点
                        q = p->next;
                        p->next = q->next;
                        free(q);
                    }
                } else {
                    q = (PolyNode*)malloc(sizeof(PolyNode));
                    q->coef = coef;
                    q->expn = expn;
                    q->next = p->next;
                    p->next = q;
                }
            } else {
                p->next = (PolyNode*)malloc(sizeof(PolyNode));
                p = p->next;
                p->coef = coef;
                p->expn = expn;
                p->next = NULL;
            }
        } else {
            head->next = (PolyNode*)malloc(sizeof(PolyNode));
            head->next->coef = coef;
            head->next->expn = expn;
            head->next->next = NULL;
        }
    }
    return head;
}
Polynomial multiply(Polynomial poly, float coef, int expn) {  //多项式与指定单项式相乘，该单项式为 coefx^expn
    PolyNode *p, *q, *Poly = (PolyNode*)malloc(sizeof(PolyNode));
    p = Poly;
    q = poly->next;
    while (q) {
        p->next = (PolyNode*)malloc(sizeof(PolyNode));
        p = p->next;
        p->coef = (q->coef*coef);
        p->expn = (q->expn + expn);
        q = q->next;
    }
    p->next = NULL;
    return Poly;
}
void add(Polynomial poly1, Polynomial poly2) {  //把 poly2 加到 poly1 上
    PolyNode *p, *q, *r;
    r = poly1;
    p = poly1->next;  //指向第一个节点
    q = poly2->next;
    poly2->next = NULL;
    while (p && q) {
        if (p->expn > q->expn) {
            r->next = p;
            p = p->next;
            r = r->next;
        } else if (p->expn < q->expn) {
            r->next = q;
            q = q->next;
            r = r->next;
        } else {
            PolyNode *t;
            p->coef += q->coef;
            if (!(p->coef > -0.000001 && p->coef < 0.000001)) //系数不为0
            {
                r->next = p;
                r = r->next;
                p = p->next;
            } else {
                t = p;
                p = p->next;
                free(t);
            }
            t = q;
            q = q->next;
            free(t);
        }
    }
    if (p)
        r->next = p;
    if (q)
        r->next = q;
}
Polynomial polySubtract(Polynomial poly1, Polynomial poly2) {  //多项式减法 poly1-poly2形成一个新的多项式
    //把poly2的系数取相反数，形成一个新的多项式
    Polynomial poly = (PolyNode*)malloc(sizeof(PolyNode)); //构造头节点
    PolyNode *p, *q;
    p = poly;
    q = poly2->next;
    while (q) {
        p->next = (PolyNode*)malloc(sizeof(PolyNode));
        p = p->next;
        p->coef = -(q->coef);  //系数取反
        p->expn = q->expn;
        q = q->next;
    }
    p->next = NULL;
    add(poly, poly1);  //利用加法
    return poly;
}
Polynomial polyAdd(Polynomial poly1, Polynomial poly2) { //多项式相加 poly1+poly2形成一个新的多项式
    Polynomial poly = (PolyNode*)malloc(sizeof(PolyNode));  //和多项式的头节点
    poly->next = NULL;
    PolyNode *p, *q, *r;
    r = poly;
    p = poly1->next;
    q = poly2->next;
    while (p&&q) {
        if (p->expn > q->expn) {
            r->next = (PolyNode*)malloc(sizeof(PolyNode));
            r = r->next;
            r->coef = p->coef;
            r->expn = p->expn;
            p = p->next;
        } else if (p->expn < q->expn) {
            r->next = (PolyNode*)malloc(sizeof(PolyNode));
            r = r->next;
            r->coef = q->coef;
            r->expn = q->expn;
            q = q->next;
        } else {
            float m = p->coef + q->coef;
            if (!(m > -0.000001 && m < 0.000001)) {
                r->next = (PolyNode*)malloc(sizeof(PolyNode));
                r = r->next;
                r->coef = m;
                r->expn = p->expn;
            }
            q = q->next;
            p = p->next;
        }
    }
    while (p) {
        r->next = (PolyNode*)malloc(sizeof(PolyNode));
        r = r->next;
        r->coef = p->coef;
        r->expn = p->expn;
        p = p->next;
    }
    while (q) {
        r->next = (PolyNode*)malloc(sizeof(PolyNode));
        r = r->next;
        r->coef = q->coef;
        r->expn = q->expn;
        q = q->next;
    }
    r->next = NULL;
    return poly;
}
Polynomial polyMultiply(Polynomial poly1, Polynomial poly2) {  //多项式相乘
    Polynomial poly = (PolyNode*)malloc(sizeof(PolyNode));  //创建多项式和的头节点
    poly->next = NULL;
    PolyNode *p;
    p = poly2->next;
    while (p) {
        add(poly, multiply(poly1, p->coef, p->expn));
        p = p->next;
    }
    return poly;
}
void printPoly(Polynomial poly) {  //打印多项式
    if (poly && poly->next) {
        PolyNode *p = poly->next;  //p指向第一个节点
        while (p->next) {
            printf("%gx^%d", p->coef, p->expn);
            p = p->next;
            if (p && (p->coef > 0))
                printf("+");
        }
        if (p->expn == 0)
            printf("%g", p->coef);   //打印常数项
        else
            printf("%gx^%d", p->coef, p->expn);
        printf("\n");
    }
}
void freePoly(Polynomial poly) {  //释放内存
    if (poly && poly->next) {
        PolyNode *p, *q;
        p = poly;
        while (p) {
            q = p->next;
            free(p);
            p = q;
        }
    }
    poly = NULL;
}
int main() {
    printf("用链表实现多项式的加减法\n");
    Polynomial poly1, poly2, poly3;
    printf("创建多项式一\n");
    poly1 = createPolynomial();
    printf("多项式一：\n");
    printPoly(poly1);
    printf("创建多项式二\n");
    poly2 = createPolynomial();
    printf("多项式二：\n");
    printPoly(poly2);
    printf("两多项式相加，和为：\n");
    poly3 = polyAdd(poly1, poly2);
    printPoly(poly3);
    freePoly(poly3);
    printf("两个多项式相乘，积为：\n");
    poly3 = polyMultiply(poly1, poly2);
    printPoly(poly3);
    freePoly(poly3);
    printf("两多项式相减，差为：\n");
    poly3 = polySubtract(poly1, poly2);
    printPoly(poly3);
    freePoly(poly1);
    freePoly(poly2);
    freePoly(poly3);
    system("pause");
    return 0;
}

窃代码不叫偷！链表一元多项式乘法, 乘法运行错误，想不通哪里的问题，求帮助

5

不带有节点的缺点，你没避开吧
之所以单链表通常会有头结点
是原因是，不带空头结点的单链表
头结点数据的插入，删除等等。
需要特殊处理
添加一个空的（非数据）头结点。
全部数据节点的处理方式就一致了，避免了特殊处理的麻烦。

20

//两个链表相加
List add(List a_list, List b_list)
的逻辑是混乱的
混合了，创新式产插入和直接插入两种方式
结果是
三个链表中，可能有个链表是互相纠缠的，二者尾部是相同的
形成如下结构

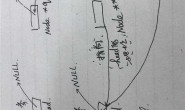
sum-> –>    P  — >NULL
^
|
i 或 j –>–>
至于乘法倒是没有这个问题，只是忽略了需要降幂（或升幂）排列的事实
同时也没有进行合并同类项的操作。
这里，忽略了多项式乘法的数学意义。
暂时就发现这么多

5

三个链表中，可能有两个链表是互相纠缠的，二者尾部是相同的
一个为和链表
一个为加数链表
其实，乘法采用插入排序的方式插入乘积，就可以做到合并同类项和 升幂，或降幂排列的目的了
实际上，鉴于多项式是升幂或降幂排列的
插入数据的时候，应该进行插入排序，
这样才能保证多项式是有序的
这比靠记忆，或有序输入做到，容易得多

5

仅供参考：

//不带表头结点的单向链表
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <time.h>
#include <locale.h>
struct NODE {
    int          data;
    struct NODE *next;
} *head,*p,*q,*s,*p1,*p2,*q1,**ta;
int i,k,n,t,m,v,N=10;
int main() {
    setlocale(LC_ALL,"chs");
    srand(time(NULL));
    head=NULL;
    printf("创建%d个节点的单链表:",N);//创建N个节点的单链表
    p=head;
    for (i=0;i<N;i++) {
        q=(struct NODE *)malloc(sizeof(struct NODE));
        if (NULL==q) exit(1);
        q->data=rand()%100;//填写0..99的随机值
        q->next=NULL;
        if (NULL==p) {
            head=q;
            p=head;
        } else {
            p->next=q;
            p=q;
        }
    }
    //输出整个单链表
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        s=s->next;
    }
    k=3;
    v=5;
    printf("将值为%d的结点插入到单链表的第%d个结点前:",v,k);//将值为v的结点插入到单链表的第k个结点前
    n=0;
    p=head;
    while (1) {
        if (NULL==p) {
            break;
        }
        n++;
        if (k==1) {
            q=(struct NODE *)malloc(sizeof(struct NODE));
            if (NULL==q) exit(1);
            q->data=v;
            q->next=head;
            head=q;
            break;
        } else {
            if (k-1==n) {
                q=(struct NODE *)malloc(sizeof(struct NODE));
                if (NULL==q) exit(1);
                q->data=v;
                q->next=p->next;
                p->next=q;
                break;
            }
        }
        p=p->next;
    }
    //输出整个单链表
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        s=s->next;
    }
    k=5;
    printf("删除第%d个节点:",k);//删除第k个节点
    n=0;
    p=head;
    while (1) {
        if (NULL==p) {
            break;
        }
        n++;
        if (k==1) {
            q=head;
            head=head->next;
            free(q);
            break;
        } else {
            if (k-1==n) {
                q=p->next;
                if (q) {
                    p->next=q->next;
                    free(q);
                }
                break;
            }
        }
        p=p->next;
    }
    //输出整个单链表
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        s=s->next;
    }
    printf("从小到大排序:");//从小到大排序
    for (p=head,p1=NULL;p!=NULL;p1=p,p=p->next) {
        for (q=p->next,q1=p;q!=NULL;q1=q,q=q->next) {
            if (p->data > q->data) {
                //交换data
//              printf("swap %02d %02d\n",p->data,q->data);
//              t=p->data;p->data=q->data;q->data=t;
                //或
                //交换next
//              printf("swap %02d %02d\n",p->data,q->data);
                if (p==head) {//p是头
                    if (p->next==q) {//pq挨着
                        head=q;
                        p->next=q->next;
                        q->next=p;
                        q=p;
                        p=head;
                    } else {//pq不挨着
                        head=q;
                        p2=p->next;
                        p->next=q->next;
                        q->next=p2;
                        q1->next=p;
                        q=p;
                        p=head;
                    }
                } else {//p不是头
                    if (p->next==q) {//pq挨着
                        p1->next=q;
                        p->next=q->next;
                        q->next=p;
                        q=p;
                        p=p1->next;
                    } else {//pq不挨着
                        p1->next=q;
                        p2=p->next;
                        p->next=q->next;
                        q->next=p2;
                        q1->next=p;
                        q=p;
                        p=p1->next;
                    }
                }
                //输出整个单链表
//              s=head;
//              while (1) {
//                  if (NULL==s) {
//                      printf("\n");
//                      break;
//                  }
//                  printf("%02d->",s->data);
//                  s=s->next;
//              }
//              getchar();
            }
        }
    }
    //输出整个单链表并计算链表长度n
    n=0;
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        n++;
        s=s->next;
    }
    printf("将整个链表逆序:");//将整个链表逆序
    if (n>=2) {
        p=head;
        q=p->next;
        p->next=NULL;
        while (1) {
            q1=q->next;
            q->next=p;
            p=q;
            q=q1;
            if (NULL==q) break;
        }
        head=p;
    }
    //输出整个单链表
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        s=s->next;
    }
    m=4;
    n=6;
    printf("将单链表中前%d个结点和后%d个结点进行互换:",m,n);//将单链表中前m个结点和后n个结点进行互换,m+n为链表总长
    k=0;
    p=head;
    while (1) {
        if (NULL==p) {
            break;
        }
        k++;
        if (m==k) {
            q=p;
        }
        s=p;
        p=p->next;
    }
    q1=head;
    head=q->next;
    s->next=q1;
    q->next=NULL;
    //输出整个单链表
    s=head;
    while (1) {
        if (NULL==s) {
            printf("\n");
            break;
        }
        printf("%02d->",s->data);
        s=s->next;
    }
    //释放全部节点
    p=head;
    while (1) {
        if (NULL==p) {
            break;
        }
        q=p->next;
        free(p);
        p=q;
    }
    return 0;
}
//创建10个节点的单链表:08->74->07->23->03->99->31->56->88->16->
//将值为5的结点插入到单链表的第3个结点前:08->74->05->07->23->03->99->31->56->88->16->
//删除第5个节点:08->74->05->07->03->99->31->56->88->16->
//从小到大排序:03->05->07->08->16->31->56->74->88->99->
//将整个链表逆序:99->88->74->56->31->16->08->07->05->03->
//将单链表中前4个结点和后6个结点进行互换:31->16->08->07->05->03->99->88->74->56->
//
CodeBye 版权所有丨如未注明 , 均为原创丨本网站采用BY-NC-SA协议进行授权 , 转载请注明链表一元多项式乘法, 乘法运行错误，想不通哪里的问题，求帮助！
喜欢 (0)赏
[1034331897@qq.com]
分享 (0)