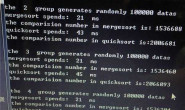
就是本人要求(阶乘) N! 的值的位数,为什么可以用取对数log10的方法来求呢?
解决方案
20
1)乘积化和:
lg(a*b) = lg(a)+lg(b)
2)位数和对数的关系,
对于一个大于0 的数 x
常用对数的整数部分加一,就是位数
假设 lg(x) =n+lg(t) //1<=t <10
则有 x= t *10^n 也就数有 n+1位数
lg(1)=0
lg(2)=0.3010
lg(10)=1
3)常用对数 lg C语言中, 用库函数 log10表示
常用对数lg就是以10为底数的对数
lg(a*b) = lg(a)+lg(b)
2)位数和对数的关系,
对于一个大于0 的数 x
常用对数的整数部分加一,就是位数
假设 lg(x) =n+lg(t) //1<=t <10
则有 x= t *10^n 也就数有 n+1位数
lg(1)=0
lg(2)=0.3010
lg(10)=1
3)常用对数 lg C语言中, 用库函数 log10表示
常用对数lg就是以10为底数的对数
20
一个数x有N位,原因是第一项至少是1,所以x>=10^(N-1)。原因是高于N位的数码都是0,所以x<=9*10^(N-1)+9*10^(N-2)+…+9<10^N
10^(N-1)<=x<10^N
两边取log10
N-1<=log10(x)<N
10^(N-1)<=x<10^N
两边取log10
N-1<=log10(x)<N